Introducción

El desarrollo de algoritmo es un tema fundamental en el diseño de programas por lo cual el alumno debe tener buenas bases que le sirvan para poder desarrollar de manera rápida y fácil sus programas.

Estos apuntes sirven de apoyo al catedrático del departamento de computación de la UCC, en su labor cotidiana de enseñar; al estudiante le ayudara a desarrollar su capacidad analítica y creadora y de esta manera mejorar su destreza en la elaboración de algoritmos que es la base de la programación  y encausaran al estudiante con la disciplina de la programación.

Objetivo Educacional

Alumno:

·         Conocerá terminología relacionada con los algoritmos, asi como la importancia de aplicar técnicas adecuada de programación.

·         Conocerá la metodología en cada una de sus etapas.

ALGORITMO

Define algoritmo como un conjunto ordenado y finito de operaciones que permite hallar la solución de un problema. Método y notación en las distintas fórmulas del cálculo. El algoritmo constituye un método para resolver un problema mediante una secuencia de pasos a seguir. Dicha secuencia puede ser expresada en forma de diagrama de flujo con el fin de seguirlo de una forma más sencilla.
Ejemplo:

TIPOS DE ALGORITMOS

Cualitativos: Son aquellos en los que se describen los pasos utilizando palabras.

• Son todos aquellos pasos o instrucciones descritos por medio de palabras que sirven para llegar a la obtención de una respuesta o solución de un problema cualquier

Cuantitativos: Son aquellos en los que se utilizan cálculos numéricos para definir los pasos del proceso.

• Son aquellos pasos o instrucciones que involucran cálculos numéricos para llegar a un resultado satisfactorio

Tipos de algoritmos de razonamiento:

Algoritmos Estáticos: son los que funcionan siempre igual, independientemente del tipo de problema tratado.

Algoritmos Adaptativos: algoritmos con cierta capacidad de aprendizaje.

Algoritmos Probabilísticos: son algoritmos que no utilizan valores de verdad booleanos sino continuos. Existen varios tipos de algoritmos probabilísticos dependiendo de su funcionamiento, pudiéndose distinguir:

§ Algoritmos numéricos: que proporcionan una solución aproximada del problema.

§ Algoritmos de Montecarlo: que pueden dar la respuesta correcta o respuesta erróneas (con probabilidad baja).

§ Algoritmos de Las Vegas: que nunca dan una respuesta incorrecta: o bien dan la respuesta correcta o informan del fallo.

Algoritmo Cotidiano: es la serie de pasos que realizamos en nuestra vida diaria para realizar las diferentes tareas y actividades comunes, desde los pasos al levantarnos, así como ir de compras, etc.

Algoritmo Voraz: un algoritmo voraz es aquel que, para resolver un determinado problema, sigue una meta heurística consistente en elegir la opción óptima en cada paso local con la esperanza de llegar a una solución general óptima.

Algoritmo Determinista: es un algoritmo que, en términos informales, es completamente predictivo si se conocen sus entradas.

Algoritmo Heurístico: es un algoritmo que abandona uno o ambos objetivos; por ejemplo, normalmente encuentran buenas soluciones, aunque no hay pruebas de que la solución no pueda ser arbitrariamente errónea en algunos casos; o se ejecuta razonablemente rápido, aunque no existe tampoco prueba de que siempre será así.

Las heurísticas generalmente son usadas cuando no existe una solución óptima bajo las restricciones dadas (tiempo, espacio, etc.), o cuando no existe del todo.

Algoritmo de escalada: la idea básica consiste en comenzar con una mala solución a un determinado problema y, repetidamente, aplicar optimizaciones a la misma hasta que esta sea óptima o satisfaga algún otro requisito.

Tipos de expresiones

􀀮Aritméticas: Los operandos que intervienen en ella son numéricos, el resultado es numérico y los operadores son aritméticos. 􀀮Lógicas: Su resultado es CIERTO o FALSO. Se construyen mediante los operadores de comparación y lógicos.

Operadores Aritméticos

Decremento --  6--

unitario

Incremento ++  7++

unitario

Resto o módulo % 68  % 2

División   / o —  / 34 / 6

Multiplicación  x * 4 * 5

Resta  - - 5 - 4

Suma  ++ 24+56

¿QUE SON LAS EXPRESIONES?

• Son el método fundamental que tiene el programador de expresar computaciones.

• Las expresiones están compuestas de operadores, operandos, paréntesis y llamadas a funciones. Los operadores pueden ser:

• Unarios: Cuando tan solo tienen un operando. Son operadores prefijos.

• Binarios: 2 Operandos. Son operadores infijos.

• Ternarios: 3 operandos.

ORDEN DE LA EVALUACIÓN DE LOS OPERADORES.

• El orden en que se evalúan los operandos viene dado por unas reglas:

• Reglas de procedencia

• Reglas de asociatividad

• Uso de paréntesis

EVALUACIÓN DE EXPRESIONES

Toda expresión regresa un valor. Si hay más de un operador, se evalúan primero operadores mayor precedencia, en caso de empate, se aplica regla asociatividad

Para evaluar una expresión no hay que hacer nada del otro mundo, pues es bien sencillo. Sólo hay que saber sumar, restar, si un número es mayor que otro

Hay tres reglas de prioridad a seguir para evaluar una expresión:

• Primero, los paréntesis (si tiene)
• Después, seguir el orden de prioridad de operadores
• Por último, si aparecen dos o más operadores iguales, se evalúan de izquierda a derecha.

Las expresiones son secuencias de constantes y/o variables separadas por operadores válidos.

Se puede construir una expresión válida por medio de :

1. Una sola constante o variable, la cual puede estar precedida por un signo + ó – .

2. Una secuencia de términos (constantes, variables, funciones) separados por operadores.

Además debe considerarse que:

Toda variable utilizada en una expresión debe tener un valor almacenado para que la expresión, al ser evaluada, dé como resultado un valor.

Cualquier constante o variable puede ser reemplazada por una llamada a una función.

Como en las expresiones matemáticas, una expresión en Pascal se evalúa de acuerdo a la precedencia de operadores

JERARQUÍA DE OPERADORES

El orden general de evaluación de los operadores de una expresión va de izquierda a derecha, con la excepción de las asignaciones que lo hacen de derecha a izquierda.

Podemos seguir las siguientes tres reglas de evaluación de expresiones:

(Regla 1) En todas las expresiones se evalúan primero las expresiones de los paréntesis más anidados (interiores unos a otros); y éstos modifican la prioridad según la cantidad de éstos, los cuales tienen que estar balanceados (el mismo número de paréntesis que abren debe ser igual al número de los paréntesis que cierran).

(Regla 2) Todas las expresiones se evalúan tomando en cuenta la jerarquía de los operadores.

(Regla 3) Todas las expresiones se evalúan de izquierda a derecha.

A continuacion anexo un video el cual sirve para entender mas lo antes mensionado:

http://youtu.be/x9dxO0Lp2xc

 

 Variables y constantes:

             Las variables son espacios reservados en la memoria que, como su nombre indica, pueden cambiar de contenido a lo largo de la ejecución de un programa. Una variable corresponde a un área reservada en la memoria principal del ordenador pudiendo ser de longitud:

• Fija.- Cuando el tamaño de la misma no variará a lo largo de la ejecución del programa. Todas las variables, sean del tipo que sean tienen longitud fija, salvo algunas excepciones — como las colecciones de otras variables (arrays) o las cadenas.
• Variable.- Cuando el tamaño de la misma puede variar a lo largo de la ejecución. Típicamente colecciones de datos.

         Una constante es un valor que no puede ser alterado durante la ejecución de un programa.

Una constante corresponde a una longitud fija de un área reservada en la memoria principal del ordenador, donde el programa almacena valores fijos.

Por ejemplo:

• El valor de pi = 3.1416

Por conveniencia, el nombre de las constantes suele escribirse en mayúsculas en la mayoría de lenguajes.

     Tipos de  datos Fundamentales.

        Hay solamente cuatro diferentes tipos de datos que consideramos más simples o primitivos. Otros tipos de datos son tipos que representan datos más complejos. Los tipos tienen que ver con la clase de dato, una variable puede alojar y determinar qué clase de operaciones se pueden desarrollar con el dato alojado en ella. En este texto, vamos a nombrar los tipos de datos en negritas. Los tipos de datos fundamentales son:

·         Caracter:Frecuentemente se les conoce como Char, porque generalmente los lenguajes de programación están en inglés. Este tipo de dato representa a los caracteres simples, como 'm'. Un tipo de dato complejo que se deriva del tipo caracter, es aquel que reúne más de un caracter y forma palabras o frases, se llama tipo cadena o string. Ejemplo: la variable nombreEmploado de tipo string puede alojar el dato ´Juancho Perineo´.

·         Entero: Los enteros están entre los tipos de datos más utilizados en los lenguajes de programación. Hay diferentes clases de números enteros y difieren por el tamaño de ellos, incluyendo enteros cortos y enteros largos. Por ejemplo, en Java, los enteros cortos se alojan en 8 bits, mientras que los enteros de tipo largo, ocupan hasta 64 bits de longitud. Los números enteros son positivos y negativos, por ejemplo -2 y 11390. Notemos que no tienen punto decimal.

·         Real. Los números reales son números con parte decimal, por ejemplo -2.0, 11390.0 y 12.45. Sin embrago, hay lenguajes de programación como NetLogo, que no hacen diferencia entre números enteros y reales cuando son exactos, como el caso de 1 y 1.0.

·         Booleano: Los valores booleanos son valores lógicos y pueden ser falso o verdadero. En estos valores se indica el verdadero con el número 1 y el falso con el 0. Algunos lenguajes de programación, como C, prefieren poner un 0 cuando es falso y cualquier otra cosa cuando es verdadero. En el lenguaje de programación Scheme, los valores lógicos son #\t y #\f y no tienen significado numérico.

El nombre que utilizan los lenguajes de programación puede ser diferente, aún cuando se trate del mismo conjunto de datos, por ejemplo, los números reales, en Pascal se llaman real y en C de llaman float.

        Operadores y Precedencia:

            La precedencia de operadores es un conjunto de reglas de JScript que controla el orden en que el compilador realiza las operaciones cuando se evalúa una expresión. Las operaciones con mayor precedencia se realizan antes que las de menor prioridad. Por ejemplo, la multiplicación se realiza antes que la suma.

            Los paréntesis en una expresión modifican el orden de evaluación determinado por la precedencia de operador. Esto significa que una expresión encerrada entre paréntesis se evalúa por completo antes de usar su valor en el resto de la expresión.

Por ejemplo:

z = 78 * (96 - 3 + 45)

En la expresión anterior hay cinco operadores: =, *, (), - y +. Según las normas de precedencia de operadores, se evalúan en el siguiente orden: (), -, +, *, =.

1.  En primer lugar se realiza la evaluación de la expresión que está encerrada entre paréntesis. Dentro de los paréntesis, hay un operador de suma y otro de resta. Ambos operadores tienen la misma precedencia y se evalúan de izquierda a derecha. Primero, se resta 3 de 96, con lo que se obtiene un resultado de 93. A continuación, se suma el número 45 a 93 y se obtiene el valor 139.

2.   A continuación se realiza la multiplicación: El número 78 se multiplica por 139, con lo que se obtiene un resultado igual a 10764.

3.   Por último se realiza la asignación: El número 10764 se asigna a z.

Construcción de expresiones:

* Literales y Variables son expresiones primitivas:

                                                          1.7 // Literal real de tipo double

                                                          sum // Variable

        Los literales e evaluan a si mismo.

        Las variables se evalúan a su valor.

* Los operadores nos permiten conbianr expresiones  primitivas y otras expresiones formadas con operadores:

1 + 2 + 3 * 1.2 + (4 + 8) / 3.0

Los operadores se caracterizan por:

El número de operadores (unarios,binarios ).

El tipo de sus operandos (p.ej. numéricos).

El tipo del valor que se generan como resultado.

 Algorimos y Diagramas de Flujo

Diagrama de Flujo

Un diagrama de flujo es la representación gráfica de un algoritmo. También se puede decir que es la representación detallada en forma gráfica de como deben realizarse los pasos en la computadora para producir resultados.

Esta representación gráfica se da cuando varios símbolos (que indican diferentes procesos en la computadora), se relacionan entre si mediante líneas que indican el orden en que se deben ejecutar los procesos. Los símbolos utilizados han sido normalizados por el instituto norteamericano de normalización (ANSI):

Recomendaciones para el diseño de Diagramas de Flujo

• Se deben usar solamente líneas de flujo horizontales y/o verticales.
• Se debe evitar el cruce de líneas utilizando los conectores.
• Se deben usar conectores sólo cuando sea necesario.
• No deben quedar líneas de flujo sin conectar.
• Se deben trazar los símbolos de manera que se puedan leer de arriba hacia abajo y de izquierda a derecha.
• Todo texto escrito dentro de un símbolo deberá ser escrito claramente, evitando el uso de muchas palabras.

 Diseño de un Algoritmo

Las características de un buen algoritmo son:

·        *  Debe tener un punto particular de inicio.

·        * Debe ser definido, no debe permitir doble interpretaciones.

·      *  Debe ser general, es decir, soporta la mayoría de las variantes que se puedan presentar en la definición de un problema.

·       *  Debe ser finito en tamaño y tiempo de la ejecución.

 Ejemplo:

Interpretar el comportamiento de las variables que inciden en un problema.

Uso de variables

Para ello nos valdremos primeramente de algunos tipos primitivos usados habitualmente como son int (entero), String (cadena de caracteres), boolean (valor booleano verdadero o falso), float (decimal simple), etc.

Prueba de Escritorio

Para explicártela tomaré como ejemplo  el algoritmo de ordenamiento de arreglos por selección. Y con él, paso a paso, y con muchas ilustraciones, construyo la prueba de escritorio.

 Las pruebas de escritorio son vitales en la formación de cualquier programador y son muchas las razones para afirmar esto, pero sólo mencionaré algunas que considero muy importantes. La primera razón es que la pruebas de escritorio son una estrategia para buscar errores en un programa, sólo con esta razón debería ser suficiente para enseñarlas. La segunda razón, es que con una prueba de escritorio se puede entender como funciona un algoritmo, otra razón que por si sola justificaría enseñar las pruebas de escritorio. Y finalmente, la razón que considero más importante; las pruebas de escritorio desarrollan habilidades cognitivas que son esenciales para toda persona que programe.

Pero volviendo al tema, como te decía en el primer párrafo me basaré en el algoritmo de selección que se usa para ordenar arreglos.

Algorimo ( Ejemplo )

Y ahora presento la prueba de escritorio de este Algoritmo:

Representación de entrada y salida de datos

Diseñar alternativas de solución a problemas.

Metodología para la solución de problemas

1. Definición del Problema

Se puede definir como una situación en la cual se trata de alcanzar una meta, y para lograrlo se debe hallar y utilizar unos medios y unas estrategias.

2. Planeación de la Solución

La mayoría de los problemas tienen algunos elementos en común, los cuales para poder plantear una excelente solución se deben tener en cuenta las siguientes pautas:

·         Estado Inicial

·         Meta : Lo que se pretende lograr

·         Conjunto de recursos : Lo que esta permitido hacer y/o utilizar

·         Dominio: Se refiere a los conocimientos, habilidades de quien va a resolverlos

    a) Definición de Variables

La operación de asignación es el modo de darle valores a una variable. La operación de asignación se presentan con el símbolo  u operador ; las operación de asignación se representa con el símbolo u operador

    b) Proceso

Elaborar un programa implica tener que realizar una serie de pasos secuenciales y cronológico que empiezan con la detección y definición del problema y conducen ala implantación del programa que lo soluciona. Los pasos a seguir serían:

1. Comprender el problema
2. Plantear la lógica
3. Codificar el programa
4. Traducir el programa a lenguaje máquina
5. Prueba del programa
6. Ejecución del programa

3. Algoritmo

    a) Diagrama de Flujo

Un diagrama de flujo es una representación gráfica de un algoritmo o de una

parte del mismo. La ventaja de utilizar un diagrama de flujo es que se le puede

construir independientemente del lenguaje de programación, pues al momento

de llevarlo a código se puede hacer en cualquier lenguaje. Dichos diagramas se

construyen utilizando ciertos símbolos de uso especial como son

rectángulos, óvalos, pequeños círculos, etc.; estos símbolos están conectados

entre sí por flechas conocidas como líneas de flujo.

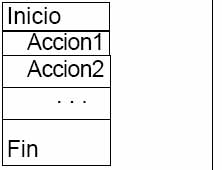
    b) Diagrama Estructurado (Nassi-Schneiderman)

El diagrama estructurado N-S también conocido como diagrama de chapin es como un diagrama de flujo en el que se omiten las flechas de unión y las cajas son contiguas. Las acciones sucesivas se pueden escribir en cajas sucesivas y como en los diagramas de flujo, se pueden escribir diferentes acciones en una caja. Un algoritmo se represente en la siguiente forma:

   

c) Pseudocódigo

Pseudocódigo Es un lenguaje artificial e informal que ayuda a los programadores a desarrollar algoritmos. El Pseudocódigo es similar al lenguaje cotidiano; es cómodo y amable con el usuario, aunque no es realmente in verdadero lenguaje de computadora. No se ejecutan en las computadoras mas bien sirven para ayudar al programadora razonar un programa antes de intentar escribirlo en algún lenguaje. Un programa ejecutado en Pseudocódigo puede ser fácilmente convertido en un programa en C++, si es que esta bien elaborado. Por ejemplo supongamos que la nota para aprobar un examen es de 60. El enunciado en Pseudocódigo sería:

Si calificación >= 60 entonces Mostrar "Aprobado" FinSi

Sentencia de entrada y salida

En programación se denominan sentencias de entrada a aquellas que permiten enviar información desde el exterior al interior de un programa y sentencias de salida a aquellas que permiten enviar información desde el interior del programa al exterior.

En los lengua­jes de progra­mación existe una gran variedad de sen­tencias de entra­da y de salida. Normalmente estas sentencias se escriben de forma distinta en función de la información, por ejemplo se escribiría de una forma si la información de entrada es numérica y de otra si la información de entrada son caracteres. También se pueden escribir las sentencias de entrada y de salida de distinta forma en función de donde reciban la información o donde la envíen (a la pantalla, a la impresora, al disco duro, a la disquetera, al diskette, a otro ordenador, a un dispositivo de control remoto, etc.).

A las sentencias de entrada y de salida se las conoce como sentencias de E/S (Entrada/Salida) o sentencias de I/O (Input/Output cuya traducción sería input = entrada y output = salida).

Sentencias de decisión.

La unidad aritmética y lógica es uno de los componentes mas importantes de una computadora típica. El propósito de la unidad aritmética es el manejo de las operaciones aritméticas; la porción lógica da a la computadora la capacidad de tomar decisiones. Esto forma la base de la construcción algoritmica if-then-else (si-entonces-de lo contrario), la que permitirá la selección de acciones alternativas.
Una decisión se especifica en una expresión lógica de la misma forma en que una operación de calculo se especifica en una expresión numérica.
Por ejemplo:

Suponga que tiene dos variables numéricas, denominadas A y B, que tienen valores diferentes, y suponga que desea imprimir el valor de la mas grande. Si A es mayor que B, debe imprimir el valor de A; pero, por otro lado, si B es mayor que A, debe imprimirse el valor de B. La elección de que alternativa tomar depende de la decisión de si la variable A es o no mayor que B. Esta estructura se representa mediante el diagrama siguiente:

1. Decisión SI.

Las estructuras selectivas se utilizan para tomar decisiones lógicas; de ahí que se suelan denominar también estructuras de decisión o alternativas.

En las estructuras selectivas se evalúa una condición y en función del resultado de la misma se realiza un opción u otra. Las condiciones se especifican usando expresiones lógicas. La representación de una estructura selectiva se hace con palabras en pseudocódigo (if, then, else o bien en español si, entonces, sino), con una figura geométrica en forma de rombo o bien con un triángulo en el interior de una caja rectangular.

Si Simple, Si Completo, Si Anidado.

Sentencias Repetitivas.

   1. Ciclo Repetitivo Mientras Que

WHILE - DO WHILE

Esta estructura nos permite repetir un bloque de instrucciones con una condición y se repite siempre en cuanto esta condición sea verdadera, sino no entra al ciclo mientras.
La estructura es la siguiente:

INICIO.
INSTRUCCION 1
MIENTRAS( CONDICION LOGICA) HAGA
INSTRUCCION 2
INSTRUCCION 3
FIN MIENTRAS
INSTRUCCION 4
FIN

El ciclo mientras (while) tiene que tener su final y salirse de el, tiene un limite y su limite es hasta que la condición ya no se cumpla, ósea que sea falsa.

EJEMPLO:

Hacer un algoritmo que lea 5 números y determine la suma entre ellos.

INICIO
ENTERO: N, i, SUMA
i=1
SUMA=0
MIESTRAS(i <=5) HAGA
MOSTRAR( 'DIGITE UN NUMERO')
LEER (N)
SUMA= SUMA+N
i= i+1
FIN MIENTRAS
MOSTRAR ('LA SUMA ES:', SUMA)
FIN

   2. Ciclo Repetitivo Para

un ciclo repetitivo donde el usuario decide cuantas veces quiere que repita una pregunta en el algoritmo. La estructura de este ciclo es la siguiente.

para( expresión lógica) expresión incrementada.

instrucción 1
instruccion2
fin para

EJEMPLO.

Un algoritmo que lea 5 números dados por un usuario y luego muestra el resultado de la suma.

INICIO
ENTERO: N, i, SUMA
SUMA=0
PARA(i= 1 HASTA ,5 , 1)
MOSTRAR ('DIGITE UN NUMERO')
LEER (N)
SUMA= SUMA+N
FIN PARA
MOSTRAR ('LA SUMA ES:', SUMA)
FIN

Donde 5 son las veces que quiero que se repita la pregunta y 1 de cuanto en cuanto se incrementa, en este casa de 1 en 1.

   3. Ciclo Repetitivo Hacer Hasta

El CICLO HAGA-MIENTRAS es similar al ciclo mientras, la diferencia radica en el momento de evaluación de la condición. En el ciclo mientras-haga la condición se evalúa antes de la ejecución del bloque, en el ciclo HAGA-MIENTRAS la condición se evalúa después de ejecutar el bloque de acciones, por lo tanto, el bloque se ejecuta por lo menos una vez. El bloque se ejecuta nuevamente si la condición evalúa a verdadero y no se ejecuta más si evalúa a falso. La forma general del ciclo HAGA-MIENTRAS es la siguiente:

haga

            <bloque de instrucciones>

mientras (condición)

Arreglos

   1. Unidimensionales (Vectores).

Son estructuras que almacenan valores del mismo tipo como números o cadenas. Tiene una longitud determinada. Lo primero es declarar su dimensión, indicando el nombre del arreglo o array y su longitud dentro de [].

Veamos un ejemplo:

1 2 3 4

Proceso Prueba     Definir num como entero;     Dimensión num[5];     FinProceso

Debemos definir num con el tipo de dato que queramos que sea, en este caso numérico, ya que si no al recorrer nos saltará un error.

En los arrays o arreglos empiezan desde 1 y acaban en la longitud que hayamos definido. Si has probado otros lenguajes de programación, sabrás que los arrays empiezan en 0 y acaban en la longitud -1 que hayamos definido. Si es tu caso lo podemos cambiar en las opciones

   2. Bidimensionales (Matrices).

Los arreglos bidimensionales son tablas de valores. Cada elemento de un arreglo bidimensional está simultáneamente en una fila y en una columna.

En matemáticas, a los arreglos bidimensionales se les llama matrices, y son muy utilizados en problemas de Ingeniería.

En un arreglo bidimensional, cada elemento tiene una posición que se identifica mediante dos índices: el de su fila y el de su columna.

Al igual que los arreglos de una dimensión, los arreglos bidimensionales también pueden ser creados usando la función array, pero pasando como argumentos una lista con las filas de la matriz:

a = array([[5.1, 7.4, 3.2, 9.9],

           [1.9, 6.8, 4.1, 2.3],

           [2.9, 6.4, 4.3, 1.4]])

Funciones o Subrutinas

Las funciones son subprogramas con 0 ó más

argumentos que siempre devuelven un valor de

retorno.

* Las funciones pertenecen entonces a un tipo

determinado.

* La invocación de una función puede formar parte

de:

* Una expresión.

* La parte derecha de una asignación.

* Una invocación de una función no puede formar:

* Una sentencia aislada.

* La parte izquierda de una asignación.

   1. Paso de parámetros por Valor.

La forma en que hemos declarado y pasado los parámetros de las funciones  es la que normalmente se conoce como "por valor". Esto quiere decir que cuando el control pasa a la función, los valores de los parámetros en la llamada se copian a "objetos" locales de la función, estos "objetos" son de hecho los propios parámetros.

Lo veremos mucho mejor con un ejemplo:

#include <iostream>

using namespace std;

int funcion(int n, int m);

int main() {

   int a, b;

   a = 10;

   b = 20;

   cout << "a,b ->" << a << ", " << b << endl;

   cout << "funcion(a,b) ->"

        << funcion(a, b) << endl;

   cout << "a,b ->" << a << ", " << b << endl;

   cout << "funcion(10,20) ->"

        << funcion(10, 20) << endl;

   return 0;

}

int funcion(int n, int m) {

   n = n + 2;

   m = m - 5;

   return n+m;

}

¿qué es lo que pasa en este ejemplo?
Empezamos haciendo a = 10 y b = 20, después llamamos a la función "función" con las objetos a y b como parámetros. Dentro de "función" esos parámetros se llaman n y m, y sus valores son modificados. Sin embargo al retornar a main, a y b conservan sus valores originales. ¿Por qué?
La respuesta es que lo que pasamos no son los objetos a y b, sino que copiamos sus valores a los objetos n y m.
Piensa, por ejemplo, en lo que pasa cuando llamamos a la función con parámetros constantes, es lo que pasa en la segunda llamada a "función". Los valores de los parámetros no pueden cambiar al retornar de "función", ya que esos valores son constantes.
Si los parámetros por valor no funcionasen así, no sería posible llamar a una función con valores constantes o literales.
  

   2. Paso de parámetros por Referencia.

Usando como ejemplo el algoritmo Multiplicación_de_dos_números_enteros del apartado Parámetros Actuales, podemos decir que en el parámetro r (variable de salida) se almacena el valor (dato) 40, como consecuencia de la instrucción de asignación:

resultado ← n1 * n2

Puede parecer que, cuando finalice el procedimiento Multiplicar, se efectuará la asignación:

r ← resultado

Pero, en realidad, resultado no es una variable que almacene un dato de tipo entero, ya que, un parámetro formal de salida, como es el caso de resultado, representa al espacio de memoria en el cual se almacena la dirección de memoria del parámetro actual correspondiente, r en este caso.

Por tanto, cuando al parámetro formal de salida (resultado) se le asigna un valor dentro del procedimiento Multiplicar. Lo que se está haciendo realmente, es asignar dicho valor al parámetro actual correspondiente (r), es decir, resultado hace referencia a r y, por tanto, se dice entonces que se está realizando un paso por referencia.